우당탕탕 개발일지
[백준] 15724. 주지수 (실버1, Pyton) 본문
반응형
풀이
1차 시도: 시간 초과
아... 너무 단순하게 생각했다.... ㅎ
그냥 무작정 범위 값을 더했다...! 하지만 시간 초과...
여기저기 찾아보니까 DP를 사용하여야 한다구 한다.
def peopleCount() :
str = input()
x1 = int(str.split(" ")[0]) - 1
y1 = int(str.split(" ")[1]) - 1
x2 = int(str.split(" ")[2]) - 1
y2 = int(str.split(" ")[3]) - 1
re = 0
for i in range(n):
if i < x1 or i > x2:
continue
for j in range(m):
if j < y1 or j > y2:
continue
re+=arr[i][j]
print(re)
s = input()
n = int(s.split(" ")[0])
m = int(s.split(" ")[1])
arr = [[0] * n for _ in range(m)]
for i in range(n):
str = input()
for j in range(m):
arr[i][j] = int(str.split(" ")[j])
ct = int(input())
for c in range(ct):
peopleCount()
2차 시도: 성공
1번 사진: 주어진 숫자 값
2번 사진: 더한 값. arr[i][j] + sumarr[i][j-1] + sumarr[i-1][j] - sumarr[i-1][j-1]

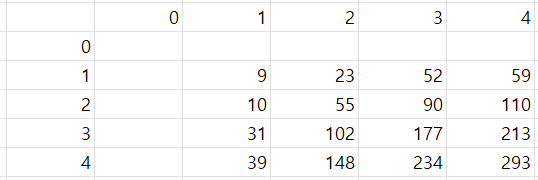
DP를 사용하려고 했는데 생각해보니 무조건 1,1에서 시작한다는 보장이 없다.
그래서 이걸 어떻게 해야 하나 고민하면서 블로그를 찾아봤다.
블로그를 보니까 첫번째 지점의 범위까지 값을 뺐다..!
예를 들어 3 3 4 4으로 주어졌다고 가정하겠다.
그러면 전체 더한 값에서 초록색 박스 부분을 빼면 된다. 하지만, 노란 박스 부분은 2번 빠지기 때문에 한번 해당 부분만 더한다.
그래서 아래와 같은 공식을 따라야 한다.
' sumarr[x2][y2] - sumarr[x2][y1-1] - sumarr[x1-1][y2] + sumarr[x1-1][y1-1] '

최종 코드
# 주지수
s = input()
n = int(s.split(" ")[0])
m = int(s.split(" ")[1])
arr = [[0] * (m+1)]
sumarr = [[0] * (m+1) for _ in range(n+1)]
for i in range(1, n+1):
str = input()
arr.append([0] + list(map(int, str.split(" "))))
for j in range(1, m+1):
# arr[i][j] = int(str.split(" ")[j])
sumarr[i][j] = arr[i][j] + sumarr[i][j-1] + sumarr[i-1][j] - sumarr[i-1][j-1]
ct = int(input())
for c in range(ct):
x1, y1, x2, y2 = map(int, input().split(" "))
t = 0
if x1 == 1 and y1 == 1:
t = sumarr[x2][y2]
else :
t = sumarr[x2][y2] - sumarr[x2][y1-1] - sumarr[x1-1][y2] + sumarr[x1-1][y1-1]
print(t)
반응형
'코테 > 백준' 카테고리의 다른 글
| [백준] 11725. 트리의 부모 찾기 (실버2, Python) (0) | 2025.06.24 |
|---|---|
| [백준] 1012. 유기농 배추 (실버2, Python) (2) | 2025.06.24 |
| [백준] 2468.안전 영역 (실버1, Python) (0) | 2025.04.21 |
| [백준] 2667.단지 번호 붙이기 (실버1, Python) (0) | 2025.04.18 |
| [백준] 2178. 미로 탐색 (실버1, Python) (1) | 2025.03.31 |




