우당탕탕 개발일지
[SWEA] 1209. [S/W 문제해결 기본] 2일차 - Sum(Java, D3) 본문
문제
다음 100X100의 2차원 배열이 주어질 때, 각 행의 합, 각 열의 합, 각 대각선의 합 중 최댓값 구하기
다음과 같은 5X5 배열에서 최댓값은 29이다.
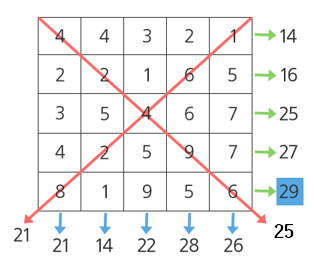
[제약 사항]
총 10개의 테스트 케이스가 주어진다.
배열의 크기는 100X100으로 동일하다.
각 행의 합은 integer 범위를 넘어가지 않는다.
동일한 최댓값이 있을 경우, 하나의 값만 출력한다.
입출력 예

풀이
2차원배열 numArr가 있다.
sum 배열의 i 에 따른 각 행의 합, 각 열의 합, 각 대각선의 합을 가지고 있다.
max배열은 현재 4가지의 최댓값을 가지고 있다.

1. 4가지 종류의 각자 합
행 : i는 동일하되 j 만 +1 씩 증가하여 한 행의 값을 모두 더함.
열 : j는 동일하되 i 만 +1 씩 증가하여 한 열의 값을 모두 더함.
왼쪽 대각선 : 각 인덱스 번호가 동일함.
오른쪽 대각선 : 첫번째는 인덱스가 +1씩 증가하고 두번째는 마지막 인덱스인 99에서 -1씩 감소함.
2. 4가지 종류의 최댓값
maxSum 배열을 사용하여 현재까지의 최댓값과 지금 더한 값을 비교하여 더 큰값을 최댓값으로 설정한다.
3. 4가지 종류의 초기화
현재의 합이 담긴 sum 배열을 0으로 초기화하여 다음 합을 구할 준비를 한다.
* 대각선의 합 설명
여기서 100 x 100이 아닌 6 x 6 으로 가정해보겠다.
아래의 그림같이 index가 변화되는 모습을 볼 수 있다. 따라서 위의 코드와 같이 각자의 대각선의 합을 구한다.

코드
Scanner sc = new Scanner(System.in);
int t=10;
for(int tc =1; tc<1+t; tc++) {
int n = sc.nextInt(); // 테스트 케이스 번호
int num = 100;
int[][] numArr = new int[num][num];
// 입력값 저장
for(int i=0; i<num; i++) {
for(int j=0; j<num; j++) {
numArr[i][j] = sc.nextInt();
}
}
int[] sum = new int[4]; // 행, 열, 왼쪽 대각선, 오른쪽 대각선
int[] maxSum = new int[4]; // 행, 열, 왼쪽 대각선, 오른쪽 대각선
// 행, 열 최대값
for(int i=0; i<100; i++) {
for(int j=0; j<100; j++) {
sum[0] += numArr[i][j]; // 행
sum[1] += numArr[j][i]; // 열
sum[2] += numArr[j][j]; // 왼쪽 대각선
sum[3] += numArr[j][num-1-j]; // 오른쪽 대각선
}
maxSum[0] = Math.max(maxSum[0], sum[0]);
maxSum[1] = Math.max(maxSum[1], sum[1]);
maxSum[2] = Math.max(maxSum[2], sum[2]);
maxSum[3] = Math.max(maxSum[3], sum[3]);
sum[0] = 0;
sum[1] = 0;
sum[2] = 0;
sum[3] = 0;
}
Arrays.sort(maxSum);
System.out.println("#"+tc+ " " + maxSum[3]);
}
SWEA 문제
https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV13_BWKACUCFAYh
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
'코테 > SW Expert Academy' 카테고리의 다른 글
| [SWEA] 13732. 정사각형 판정(Java, D3) (0) | 2024.05.21 |
|---|---|
| [SWEA] 6190. 정곤이의 단조 증가하는 수(Java, D3) (0) | 2024.05.18 |
| [SWEA] 2805. 농작물 수확하기(Java, D3) (0) | 2024.05.17 |
| [SWEA] 1208. [S/W 문제해결 기본] 1일차 - Flatten(Java, D3) (0) | 2024.05.17 |
| [SWEA] 1206. [S/W 문제해결 기본] 1일차 - View(Java, D3) (0) | 2024.05.17 |




